因式分解可以很复杂！

在上一篇的因式分解之Introduction中，因式分解给出的例子都很简单，但因式分解也可以更复杂！

因为你要猜 什么式子的积 等于已知的一个式子！

这有点像找出什么材料使一个蛋糕好吃。有时这绝对不明显！

 

运用恒等式

例子：分解 4×2 – 9

嗯。。。。。。看不到有什么因式。

可是，若你了解特别二项式乘积，你也许会看到它是 “平方差”：

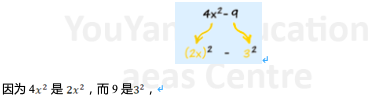
所以：

4   – 9 =  –

我们可以用这个平方差公式：

(a+b)(a-b) = –

其中 a 是 2x，而 b 是 3。

我们来试试看：

(2x+3)(2x-3) = –  =  – 9

故此，4  – 9 的因式是 (2x+3) 和 (2x-3)：

答案： 4  – 9 = (2x+3)(2x-3)

 

怎样才可以懂得这样做？做大量练习，并牢记 “恒等式”!

 

记着这些恒等式

一下是常见的 “恒等式”（包括上面用的 “平方差“）。

记着这些会对因式分解很有帮助。

a2 − b2	=	(a+b)(a−b)
a2 + 2ab + b2	=	(a+b)(a+b)
a2 − 2ab + b2	=	(a−b)(a−b)
a3 + b3	=	(a+b)(a2−ab+b2)
a3 − b3	=	(a−b)(a2+ab+b2)
a3+3a2b+3ab2+b3	=	(a+b)3
a3−3a2b+3ab2−b3	=	(a−b)3